How do you find the approximate area of a rectangle?
Table of Contents
- How do you find the approximate area of a rectangle?
- How do you do midpoint approximation?
- How do you find the approximate area?
- What is the method of midpoint rectangles?
- What is an inscribed rectangle?
- What is approximate area?
- How do you find a midpoint?
- What is the approximate area of the circle?
- How do you find the midpoint of an area?
- Which is the best way to approximate the area of a rectangle?
- Why are midpoint rectangles used to estimate area?
- Which is better a midpoint sum or a left rectangle?
- How to approximate the area under a curve?
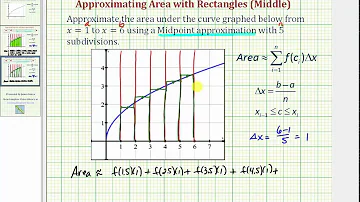
How do you find the approximate area of a rectangle?
7:049:19Approximating Area Under a Graph Using Rectangles - YouTubeYouTubeStart of suggested clipEnd of suggested clipThen the area under the curve is going to be approximately equal to the sum of f of C sub I timesMoreThen the area under the curve is going to be approximately equal to the sum of f of C sub I times Delta X where these products represent the area of rectangles.
How do you do midpoint approximation?
1: The midpoint rule approximates the area between the graph of f(x) and the x-axis by summing the areas of rectangles with midpoints that are points on f(x). Use the midpoint rule to estimate ∫10x2dx using four subintervals. Compare the result with the actual value of this integral.
How do you find the approximate area?
1:393:52How to Find Approximate Area Using Sigma Notation For Dummies ...YouTubeStart of suggested clipEnd of suggested clipStarting with the curve x squared plus 1 work this out for the six right rectangles. You areMoreStarting with the curve x squared plus 1 work this out for the six right rectangles. You are approximating the area under x squared plus 1 between 0 and 3 with 6 rectangles.
What is the method of midpoint rectangles?
The midpoint rule, also known as the rectangle method or mid-ordinate rule, is used to approximate the area under a simple curve. There are other methods to approximate the area, such as the left rectangle or right rectangle sum, but the midpoint rule gives the better estimate compared to the two methods.
What is an inscribed rectangle?
An inscribed rectangle is a rectangle drawn within a shape. In calculus, we're mostly concerned with the largest inscribed rectangle; The largest that doesn't break through the edges of the shape.
What is approximate area?
We find the area of each rectangle by multiplying the height by the width. Then, the sum of the rectangular areas approximates the area between f(x) and the x-axis. When the left endpoints are used to calculate height, we have a left-endpoint approximation.
How do you find a midpoint?
To find the midpoint, draw the number line that contains points and . Then calculate the distance between the two points. In this case, the distance between and is . By dividing the distance between the two points by 2, you establish the distance from one point to the midpoint.
What is the approximate area of the circle?
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.1416.
How do you find the midpoint of an area?
A good way to approximate areas with rectangles is to make each rectangle cross the curve at the midpoint of that rectangles top side. A midpoint sum is a much better estimate of area than either a left-rectangle or right-rectangle sum.
Which is the best way to approximate the area of a rectangle?
A good way to approximate areas with rectangles is to make each rectangle cross the curve at the midpoint of that rectangle’s top side. A midpoint sum is a much better estimate of area than either a left-rectangle or right-rectangle sum. The below figure shows why.
Why are midpoint rectangles used to estimate area?
You can see in the figure that the part of each rectangle that’s above the curve looks about the same size as the gap between the rectangle and the curve. A midpoint sum produces such a good estimate because these two errors roughly cancel out each other. The figure above shows how you’d use three midpoint rectangles to estimate the area under
Which is better a midpoint sum or a left rectangle?
A midpoint sum is a much better estimate of area than either a left-rectangle or right-rectangle sum. The below figure shows why. You can see in the figure that the part of each rectangle that’s above the curve looks about the same size as the gap between the rectangle and the curve.
How to approximate the area under a curve?
When finding the area under a curve for a region, it is often easiest to approximate area using a summation series. This approximation is a summation of areas of rectangles. The rectangles can be either left-handed or right-handed and, depending on the concavity, will either overestimate or underestimate the true area.

 Main Topics
Main Topics


