Can you take the derivative of a vector?
Table of Contents
- Can you take the derivative of a vector?
- Can a function be its own derivative?
- What is the derivative of the vector function?
- How do you find the vector value of a function?
- How do you integrate a vector function?
- How do you prove a derivative?
- What is the derivative of 2x?
- How do you know if a function is vector valued or scalar valued?
- Can an integral be a vector?
- Which is the derivative of a vector function?
- Why are there limits on a vector function?
- How to calculate the definite integral of a vector function?
- Can a product rule be extended to vector valued functions?
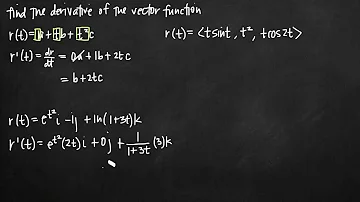
Can you take the derivative of a vector?
To take the derivative of a vector-valued function, take the derivative of each component. If you interpret the initial function as giving the position of a particle as a function of time, the derivative gives the velocity vector of that particle as a function of time.
Can a function be its own derivative?
The derivative of an exponential function is a constant times itself. Using this definition, we see that the function has the following truly remarkable property. Hence is its own derivative. In other words, the slope of the plot of is the same as its height, or the same as its second coordinate.
What is the derivative of the vector function?
The derivative of a vector-valued function can be understood to be an instantaneous rate of change as well; for example, when the function represents the position of an object at a given point in time, the derivative represents its velocity at that same point in time.
How do you find the vector value of a function?
A vector-valued function is a function of the form ⇀r(t)=f(t)ˆi+g(t)ˆj or ⇀r(t)=f(t)ˆi+g(t)ˆj+h(t)ˆk, where the component functions f, g, and h are real-valued functions of the parameter t. The graph of a vector-valued function of the form ⇀r(t)=f(t)ˆi+g(t)ˆj is called a plane curve.
How do you integrate a vector function?
5:139:05Integral of the vector function (KristaKingMath) - YouTubeYouTube
How do you prove a derivative?
Proof of Sum/Difference of Two Functions : (f(x)±g(x))′=f′(x)±g′(x) This is easy enough to prove using the definition of the derivative. We'll start with the sum of two functions. First plug the sum into the definition of the derivative and rewrite the numerator a little.
What is the derivative of 2x?
Since the derivative of cx is c, it follows that the derivative of 2x is 2.
How do you know if a function is vector valued or scalar valued?
A scalar function is a real-valued function. Note that if u(t) is a scalar function and f(t) is a vector-valued function, then their product, defined by (uf)(t)=u(t)f(t) for all t, is a vector-valued function (since the product of a scalar with a vector is a vector).
Can an integral be a vector?
The definite integral of a continuous vector function r(t) can be defined in much the same way as for real-valued functions except that the integral is a vector. This means that we can evaluate an integral of a vector function by integrating each component function.
Which is the derivative of a vector function?
Definition: Derivative of Vector-Valued Functions. The derivative of a vector-valued function ⇀ r(t) is. ⇀ r′ (t) = lim Δt → 0 ⇀ r(t + Δt) − ⇀ r(t) Δt. provided the limit exists. If ⇀ r ′ (t) exists, then ⇀ r(t) is differentiable at t.
Why are there limits on a vector function?
Objectives Limits were developed to formalize the idea of a derivative and an integral. Now that we have defined how limits work for vector functions, we know how to define how derivatives and integrals work. Because limits distribute through to the components of the vector, the same is true for derivatives and integrals.
How to calculate the definite integral of a vector function?
Calculate the definite integral of a vector-valued function. To study the calculus of vector-valued functions, we follow a similar path to the one we took in studying real-valued functions. First, we define the derivative, then we examine applications of the derivative, then we move on to defining integrals.
Can a product rule be extended to vector valued functions?
1. We can extend to vector-valued functions the properties of the derivative that we presented previously. In particular, the constant multiple rule, the sum and difference rules, the product rule, and the chain rule all extend to vector-valued functions. However, in the case of the product rule, there are actually three extensions:

 Main Topics
Main Topics